这是一个创建于 1171 天前的主题,其中的信息可能已经有所发展或是发生改变。
之前在看课的时候学到一个概念叫 Benford's law ,用来描述真实数字数据集中首位数字的频率分布,数字越大出现概率越低,比如以 1 为首位数字的数的出现概率约为总数的三成。但有个前提,这些数字必须是没有范围限制且没有人为干预的,举个例子电话号码就明显不符合。
那么,这一定律在疫情数据上表现如何呢?
我简单做了一个数据 app 来看各国分布与标准分布的差距,仅供娱乐 👇
https://benfords-law-covid19.streamlitapp.com/
预览:
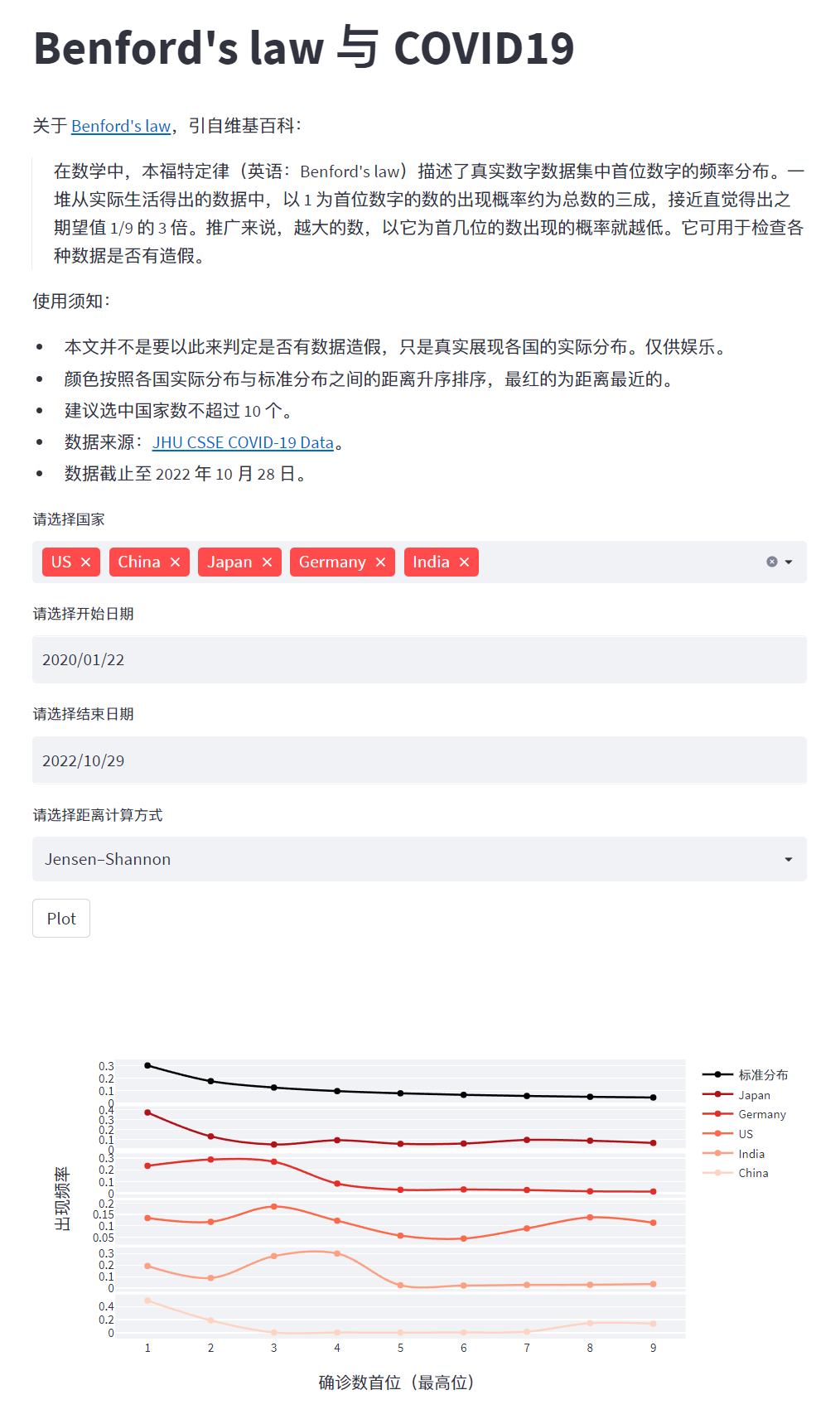
第 1 条附言 · 2022 年 10 月 31 日
我在 App 中第一条就说明了仅供娱乐,道理不是只有你一个人懂,有些人请嘴巴上放干净,气不过请 block 。
1
Macolor21 2022 年 10 月 31 日 大胆!
|
2
ruxuan1306 2022 年 10 月 31 日
国内确诊人数肯定是远高于卫健委统计值的,就和失业率一样。
|
3
luckykong 2022 年 10 月 31 日
哈。。你们有没有看数据到底揭示了什么结果?
|
4
cmos 2022 年 10 月 31 日 via Android 本福特“定律”应用的前提是事件之间没有依赖 /从属关系,医疗事件具有群体性、地域性和时空性,加上疫情本身被人力干涉。我在生物医学行业这么多年,从来没有见过哪个医学人员会用这玩意去说明事情。按照你这个逻辑,拜登选票也不符合本福特定律。你这么干,和拿绿茶送检,然后宣布医院说绿茶有糖尿病一样离谱。
|
5
cmos 2022 年 10 月 31 日 via Android @imes 4# [补充] 再贴一个知乎的解释,说明为什么这玩意不可靠( https://www.zhihu.com/question/49661986/answer/1565667783 ),已经很简洁易懂了。学医,最忌讳看到了的新东西,就瞎 jb 乱用。
|
7
Leviathann 2022 年 10 月 31 日
然后他们看到了,说对,现有的清零政策导致了这些假数据,要加大力度真正做到清零。
或者 lz 本来就是清零派? |
8
Zhengqing 2022 年 11 月 1 日 via iPhone
挺好玩
|
9
albert0yyyy 2022 年 11 月 1 日
反思,立刻就反思
|